1 Introduction
In this paper, we study the identification of unique users among
a set of online pseudonyms, based on content analysis.
Specifically, we consider the problem of reverse engineering the
multiple aliases belonging to an individual based on text posted by
those aliases in public fora such as bulletin boards, netnews,
weblogs, or web pages.
Beginning with Chaum's work on digital pseudonymous
identities [3,4], there has been significant work on
mechanisms to provide aliases that cannot be penetrated or linked
through examination of network transmission data. Systems such as
Onion Routing [16],
Crowds [17], Freedom [18], and LPWA [9] have moved network
pseudonyms from an academic interest to a reality. However, even
after all network artifacts have been removed, certain classes of
pseudonyms remain vulnerable to identity detection [14]. This vulnerability stems
from the fundamental role of participants in an online world: to
provide value, the distinct pseudonyms must engage in interactions
that are likely to be information-rich, and are hence susceptible
to a new set of attacks whose success properties are not yet well
understood.
On the other hand, research in economics and game theory has
focused [8] on the
social cost resulting from the widespread availability of
inexpensive pseudonyms. A user can readily open a hundred email
accounts at a free service such as Yahoo! or Hotmail, while
masquerading under a hundred different identities at an online
marketplace such as eBay or ePinions. The power of a system without
enforcement mechanisms or registries comes with the potential for
various forms of abuse.
Research in the field of reputation networks attempts to
devise trust mechanisms that make it unlikely that a mountebank who
preys on innocent people (say in an online marketplace) will garner
the level of trust needed to command an effective economic premium
for goods or services (i.e., if the same merchandise is sold by two
individuals of different trust levels, the one with the higher
trust value commands a higher price - this effect is visible in
online marketplaces such as eBay).
We focus on aliases used by individuals in order to post on
online bulletin boards. Users on these boards adopt multiple
aliases for many different reasons. In some cases, an old alias has
been banned by a moderator, or a password has been forgotten. In
others, an old alias has lost the trust of the group, developed bad
personal relationships with members of the group, or still exists,
but requires an alter ego to support his arguments. Some
users enjoy creating aliases that can take different sides, or can
express different personalities (sometimes from the perspective of
different genders). And some aliases allow a user to take on a
reasonable or an extreme position in turn. Finally, of course, some
users wish to express questionable or socially unacceptable views,
or wish to discuss immoral or illegal activities.
Our main contribution is to establish that techniques from data
mining and machine learning, when carefully tuned, can be surprisingly
effective at detecting such aliases, to the extent that our perception of
the privacy afforded by aliasing mechanisms may be optimistic.
In the language of machine learning, we seek to ``cluster''
aliases into equivalence classes, where the aliases in a class are
all deemed by the system to be the same user. A system to perform
such a clustering must address two underlying problems. First,
given some characterization of the content authored by an alias,
and given new content, it must determine the likelihood that the
alias produced the new content. And second, given such a primitive
for computing likelihoods, it must determine the most appropriate
clustering of aliases into authors. We show that in each case,
algorithms tailored to the scope and nature of the domain perform
significantly better than classical techniques.
First, we studied several mechanisms for ranking a set of
authors by likelihood of having generated a particular dataset.
Given 100 authors (synthetically) split into 200 aliases, our best
similarity measure ranks an author as most similar to her paired
alias (out of 199 candidates) 87% of the time. In order to attain
this result, we consider a number of different feature sets and
similarity measures based on machine learning and information
theory.
Next, we explore algorithms for clustering given this
combination of features and the notion of similarity. For this we
require a measure for comparing two clusterings, to evaluate how
well our algorithm (as well as alternatives) perform relative to
the ground truth. One of our contributions is the development of a
clean 2-dimensional measure motivated by the concepts of precision
and recall that are fundamental in information retrieval. We
believe that for settings such as ours, this measure is more
natural for evaluating the effectiveness of a clustering scheme
than traditional measures.
On the previously mentioned set of 100 two-element clusters, we
achieve the perfect cluster (i.e., contains all aliases, and no new
aliases) 92% of the time if our clustering algorithm is terminated
after it produces 100 clusters. We also give results for different
distributions of cluster sizes and numbers of aliases.
Finally, we consider the problem of automatically stopping the
clustering process at the ``right'' point - this would be the
setting when we do not have a synthetic dataset (with a known
target number of alias clusters). We present a clean and natural
stopping condition for this problem that requires no outside
parameterization. On the benchmark described above, this condition
achieves a figure of merit within 2% of the optimal stopping
point.
These results are attained using significantly less data per
alias than other studies in the area, and achieve error rates that
are substantially lower than other published reports.
We begin in Section ![[*]](p432-novak-crossref.png) by covering related work. In
Section
by covering related work. In
Section ![[*]](p432-novak-crossref.png) we
develop our similarity measure capturing the likelihood that each
author in the system generated a particular collection of text.
Next, in Section
we
develop our similarity measure capturing the likelihood that each
author in the system generated a particular collection of text.
Next, in Section ![[*]](p432-novak-crossref.png) we describe combining
the output of the similarity measure into a clustering of aliases
representing the underlying individuals. In Section
we describe combining
the output of the similarity measure into a clustering of aliases
representing the underlying individuals. In Section ![[*]](p432-novak-crossref.png) , we describe a case study
moving from our analytical domain into a real world bulletin board
with no planted clusters.
, we describe a case study
moving from our analytical domain into a real world bulletin board
with no planted clusters.
2 Related Work
The field of author analysis, or stylometrics, is best
known for its detailed analysis of the works of
Shakespeare [2,22], its success in resolving
the authorship of the Federalist Papers [13], and its recent success in
determining the author of the popular novel Primary Colors.
Our problem is somewhat different - rather than determine which of
several authors could have written a piece of text, we wish to
extract from dozens of online identities a smaller set of
underlying authors. Diederich et al. [6] used SVM classifiers
to learn authorship of newspaper articles; de Vel et
al. [5] and Tsuboi
and Matsumoto [19] used
the same technique for email messages. Argamon et al. [1] studied matching newspaper
articles back to the newspaper. Krsul and Spafford [10] performed author
identification on C programs rather than traditional documents,
using features such as comments, indentations, case and so
forth.
Most similar to our work, Rao and Rohatgi [14] study netnews postings
and use PCA and a nearest-neighbor-based clustering algorithm to
attain an almost 60% success rate at merging 117 users with two
aliases each back into their original classes. They concluded that
users are safe from anti-aliasing if fewer than 6500 words of text
exist for the user. Our results in contrast indicate that for the
data in our corpus, and the algorithms we develop, significantly
less text enables significantly higher accuracy.
Grouping aliases into authors fits the general paradigm of
agglomerative clustering algorithms [20,21] from machine learning.
Here one begins with a set of entities (say documents) each in its
own cluster, then repeatedly agglomerates the two
``closest'' clusters into one - thereby diminishing the total
number of clusters by one (at each agglomeration step). An
important piece of this process is deciding when to halt the
process of agglomeration; see [15,11] for some discussion.
3 Data
For our experiments, we gathered postings from message board
archives on http://www.courttv.com. Posters on the
CourtTV message boards tend to be highly engaged, posting
frequently and emotionally, and use of multiple pseudonyms is quite
common. We first crawled the homepage for the message boards
http://www.courttv.com/message_boards to get a
list of available topics. We then picked several topics of
discussion: the Laci Peterson Case, the War in Iraq, and the Kobe
Bryant case. Our selections were motivated by the volume of posting
on the board, and our assessment of the likelihood that posters on
the board would adopt aliases in their postings.
For each topic, we crawled the topic homepage to generate a list
of thread URLs, which we then crawled to generate a list of pages
of postings. We then crawled and parsed the postings pages. We
broke the resulting content into individual posts, and extracted
metadata such as the alias of the poster and the date and time of
the post.
Our preliminary methodology to evaluate the effectiveness of our
algorithms is to gather a large number of posts from a series of
aliases, split each alias into smaller sub-aliases, then ask the
algorithm to piece the sub-aliases back together
(see [14] for an
earlier application of this technique). Thus, careful data cleaning
is extremely important to guarantee that the algorithm does not
``cheat'' by using, for example, the signature at the end of each
post as a highly discriminant feature. Thus, we removed signatures,
titles, headers from inclusions of other messages, and any quoted
content copied from other postings. When considering word counts
and misspellings as features, we also removed any HTML tags and
lowercased the remaining text. We then scanned a large number of
postings by hand to verify that no additional hidden features based
on the current alias remained.
Many users included emoticons, or ``smilies'' in their postings.
These gif images were easily identifiable as they were included
from a common directory (http://board1.courrtv.com/smilies). We
included counts of usage of each type of smiley to our set of
features. After computing the frequency of words, misspellings,
punctuation and emoticons for each posting as described below, we
accumulated the results to create a record of features for each
user.
Each message board contained a large number of postings (323K
postings on the Laci board at the time of our crawl), and a large
number of users (3000 on the Laci board), so we had a range in the
number of users and number of messages to use in our experiments.
While our results improved as we analyzed more messages per alias,
we sought to identify authors with a minimal amount of data. Except
as noted, for all experiments cited in this paper we used 50
messages per alias totaling an average of 3000 words.
In the following, we will use the term alias or pseudonym
interchangeably. Conversely, we will use the term author to refer
to the underlying individual, who may employ a single alias or
several of them.
4 Similarity Measures
Our goal in this section is to develop a directed
similarity measure to capture the likelihood that the author of the
text in one corpus would have generated the text in a second
corpus. By directed we refer to fact that these likelihoods are not
symmetric between pieces of text. In Section ![[*]](p432-novak-crossref.png) , we will use the
resulting similarity measure to cluster aliases together.
, we will use the
resulting similarity measure to cluster aliases together.
We begin by considering the appropriate set of features to use.
Next, we turn to algorithms for determining similarity given a
fixed feature set.
As input from our data gathering process we are given a set of
aliases, and for each alias, a set of posts with associated
metadata. We refer to the collection of posts as the corpus for
that particular alias.
From the corpus for each alias, we must now extract the features
that we will use to characterize the corpus going forward.
Stylometers argue that there are certain stylistic features that an
author cannot choose to obscure, and that these features remain
relatively constant from domain to domain for the same author. The
two most commonly used feature classes in the stylometry literature
are the following: first, numerical measures such as the mean and
standard deviation of word, sentence, and paragraph length; and
second, the distribution of words within a relatively small number
of sets of function words (frequent content-free words whose
occurrence frequency does not change much from domain to
domain1). However, these features are
typically used to ascribe very large collections of highly
ambiguous text to a small number of possible authors (often 2 to
5), while our goal is to map much smaller amounts of more specific
language to a much larger population of authors, so we must broaden
the range of permissible features.
After some experimentation, we chose to model the feature set
representing the corpus of a particular alias by the following four
distributions:
- Words:
- After detagging, words are produced by tokenizing on
whitespace. We do fold all words into lowercase, but we do not
perform stemming.
- Misspellings:
- Words that are not in a large dictionary.
- Punctuation:
- Any of the common punctuation symbols.
- Emoticons:
- Any of the emoticon images allowed by CourtTV.
- Function Words:
- Described above.
Figure ![[*]](p432-novak-crossref.png) shows the results of an experiment comparing each of the four
feature distributions. For this experiment, we took 100 aliases
with at least 100 posts each from the Laci Peterson message board.
We split each alias into two sub-aliases of 50 posts each, broken
at random. For each of the resulting 200 sub-aliases, we applied
the selected feature extractor to the alias. We then employed the
KL similarity measure defined below; this is our best-performing
measure, used here to benchmark the different feature sets. For
each sub-alias a, we compute the similarity between a
and the other 199 sub-aliases, and sort the results. The figure
shows the probability that a's matching sub-alias was ranked
first out of the 199 candidates.
shows the results of an experiment comparing each of the four
feature distributions. For this experiment, we took 100 aliases
with at least 100 posts each from the Laci Peterson message board.
We split each alias into two sub-aliases of 50 posts each, broken
at random. For each of the resulting 200 sub-aliases, we applied
the selected feature extractor to the alias. We then employed the
KL similarity measure defined below; this is our best-performing
measure, used here to benchmark the different feature sets. For
each sub-alias a, we compute the similarity between a
and the other 199 sub-aliases, and sort the results. The figure
shows the probability that a's matching sub-alias was ranked
first out of the 199 candidates.
There are a few messages to take away from the figure. First,
words are clearly the most effective feature set, so much so that
we have focused entirely on them for the remainder of the
discussion. Second, it should be possible to extend our techniques
to merge the different feature sets together gracefully, perhaps
attaining an even higher overall result, but we have not taken this
path. Third, our success probabilities are dramatically greater
than in traditional stylometry: in that field, 90% probability of
correctly identifying one of five authors given a large amount of
text for the classification is considered an excellent result. This
is due perhaps in part to our algorithms, but certainly largely due
to the fact that personas on the web are much more distinguishable
than William Thackeray and Jane Austen.
Figure: Evaluation of
Different Feature Sets.
|
|
There are a number of additional features that appear powerful,
that were beyond our scope to analyze. These include: correlation
of posting times; analysis of signature files; clustering of
misspellings; references to entities such as people, locations, and
organizations; expressed relationships such as daughter, husband,
etc.; use of blank lines, indentations and other formatting cues;
use of HTML tags such as fonts, colors, or links; and use of
capitalization. A comprehensive treatment of these would entail
augmenting our feature set with hidden markov models (for temporal
features), link analysis (for references) and some entity
extraction. Such detailed analyses would likely lower our already
low error rates; our goal here is to demonstrate that even our
simpler set of features suffice to viably jeopardize privacy
derived from aliases.
Let A be the set of all aliases, and let n = |
A|. Let a be an alias, and pa be
the feature vector for the alias using the word feature set: each
dimension in pa represents a word, and the entry
corresponds to the probability of that word in a's corpus,
so
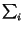 pa(i) = 1. Next, let
pa(i) = 1. Next, let
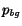 be the background
distribution of word occurrences across all text from all
aliases.
be the background
distribution of word occurrences across all text from all
aliases.
We now present three algorithms for similarity. We note that the
similarity measure produced need not be symmetric, so
Sim(a, b) need not be Sim(b,
a). The interpretation is that Sim(a,
b) is the likelihood that the text in the corpus of alias
a could have been produced by the author of the text for
alias b.
This measure is based on the standard information retrieval
cosine similarity measure [7]. We define va to
be a vector corresponding to alias a with appropriate
weighting for the measure, as follows:
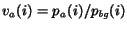 .
.
The definition of the measure is:
SimTF/IDF(
a,
b)
=
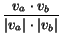
.
The KL divergence of two distributions is defined as follows:
D(
p||
q) =
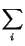 pi
pi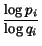
.
The KL divergence measures the number of extra bits that must be
used to encode distribution p if instead of constructing the
best possible code for p, we instead use the optimal code
for distribution q. Intuitively, this seems to capture the
notion that the author of q might have produced the text of
p if that text can be encoded efficiently assuming it was in
fact generated by q. The definition of the measure, then, is
the following:
SimKL(a, b) =
D(pa|| pb)
where the distributions pa and
pb are smoothed according to the discussion in
Section ![[*]](p432-novak-crossref.png) ,
but the measure is computed only on non-zero elements of the
original pa.
,
but the measure is computed only on non-zero elements of the
original pa.
This measure also has a probabilistic interpretation in our
framework. Consider the corpus of alias a 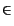 A as a sequence of words
w1, w2,...,
wn. The probability that b would have
generated that sequence in that order is simply
A as a sequence of words
w1, w2,...,
wn. The probability that b would have
generated that sequence in that order is simply
![$ \Pi_{{j\in[1..n]}}^{}$](p432-novak-img8.png) pb(wj).
Assuming that the corpus of a has size n, and the
distinct words are given in W, then the number of
occurrences of word i in the corpus is
npa(i), and the total probability that
b would generate the corpus is given by
pb(wj).
Assuming that the corpus of a has size n, and the
distinct words are given in W, then the number of
occurrences of word i in the corpus is
npa(i), and the total probability that
b would generate the corpus is given by

=
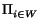 pb
pb(
i)
npa(i).
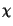 = n
= n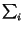 pa(i)log p
b(i). We observe that
D(pa|| pb) =
H(pa) - log
pa(i)log p
b(i). We observe that
D(pa|| pb) =
H(pa) - log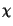 /n. The terms H(pa) and
n are both independent of b, so the ranking induced
by maximizing the probability of b generating the corpus of
a, over all b, is the same as the ranking induced by
minimizing the KL divergence.
/n. The terms H(pa) and
n are both independent of b, so the ranking induced
by maximizing the probability of b generating the corpus of
a, over all b, is the same as the ranking induced by
minimizing the KL divergence.
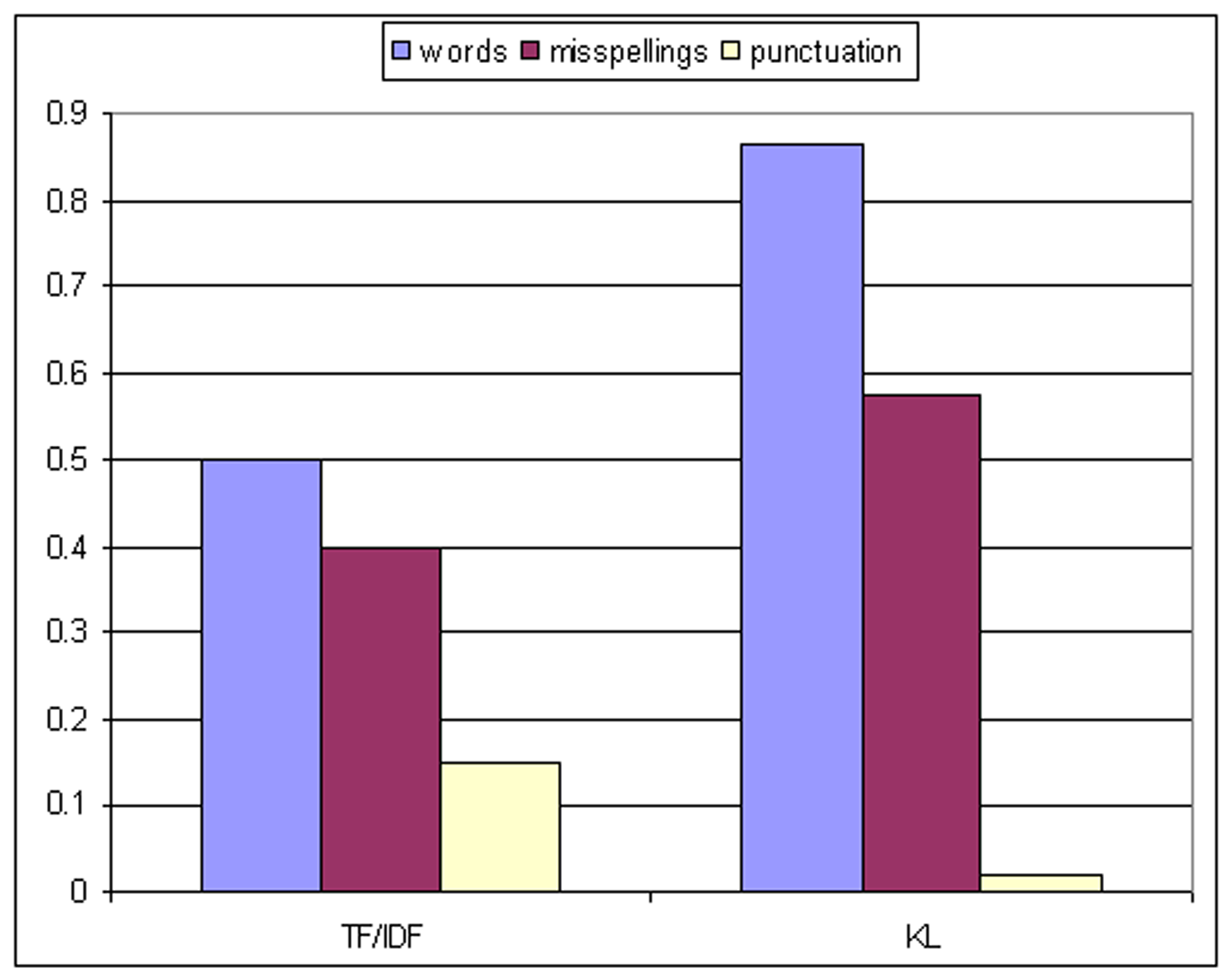
Results for these algorithms are shown in Figure ![[*]](p432-novak-crossref.png) . They show that
SimKL performs significantly better than does
SimTF/IDF, so we will adopt the KL measure going
forward. Using the benchmark described above, and using words as
our feature, the algorithm ranks the correct alias first out of 199
possibilities 88% of the time.
. They show that
SimKL performs significantly better than does
SimTF/IDF, so we will adopt the KL measure going
forward. Using the benchmark described above, and using words as
our feature, the algorithm ranks the correct alias first out of 199
possibilities 88% of the time.
Figure: Evaluation of
Similarity Algorithms.
|
|
4.4 Smoothing
In presenting Figure ![[*]](p432-novak-crossref.png) , we must mention one
critical modification to the measure: that of smoothing
the probability distribution defined by each feature vector. This
is a standard concern whenever a probabilistic generative model is
used to characterize content: how should we deal with two authors
a and b who might be the same person, if the sample
content from a doesn't use a particular word that b
used (and vice versa)? A model without smoothing would assign zero
probability to the event that a generated b's
output.
, we must mention one
critical modification to the measure: that of smoothing
the probability distribution defined by each feature vector. This
is a standard concern whenever a probabilistic generative model is
used to characterize content: how should we deal with two authors
a and b who might be the same person, if the sample
content from a doesn't use a particular word that b
used (and vice versa)? A model without smoothing would assign zero
probability to the event that a generated b's
output.
There are a number of traditional approaches to smoothing; we
use the simple approach of taking a linear combination of
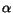 times a's
distribution over features with 1 -
times a's
distribution over features with 1 - 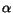 times the background distribution over features. The
only parameter to study is therefore the weight
times the background distribution over features. The
only parameter to study is therefore the weight 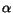 in the linear combination.
in the linear combination.
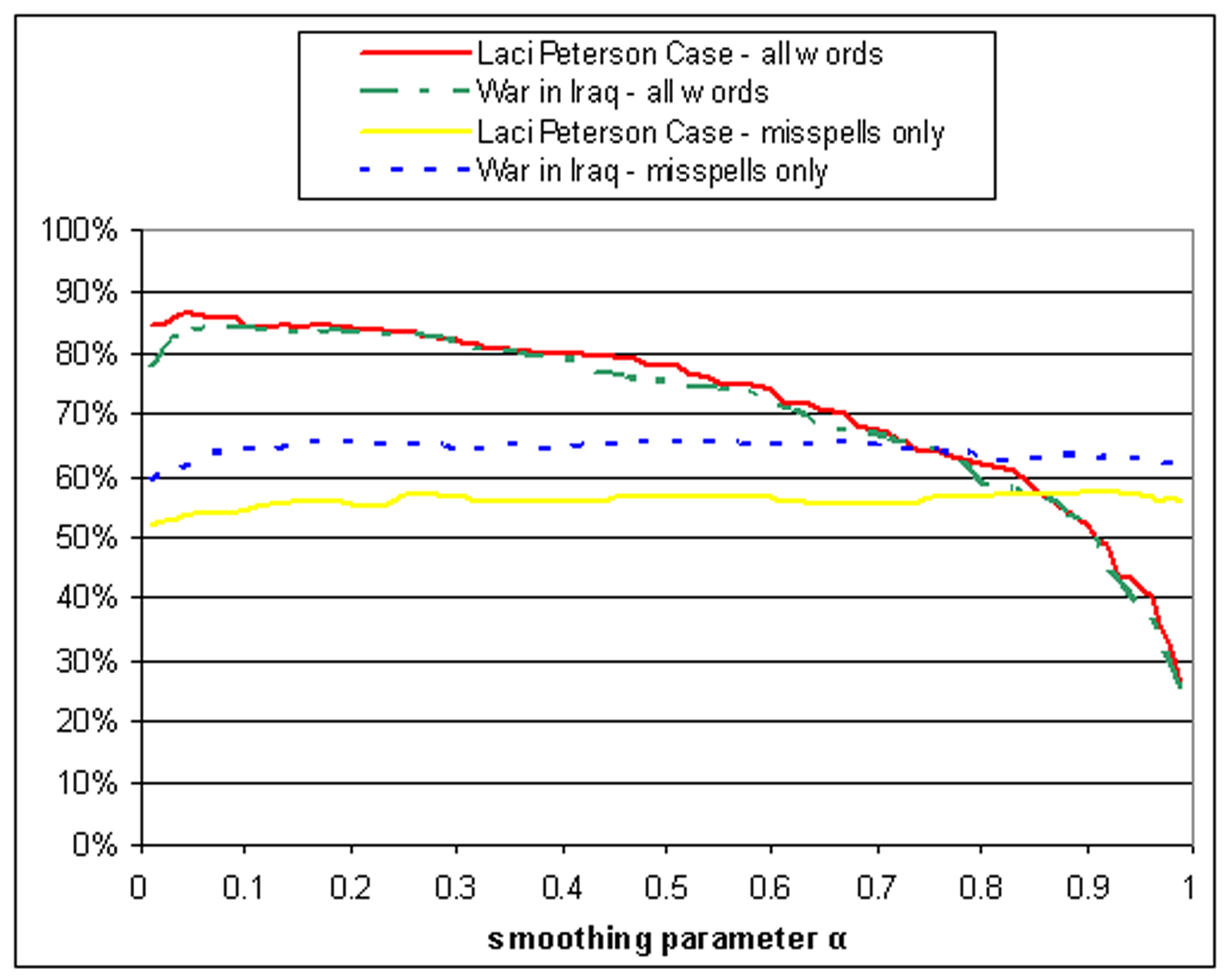
In the literature, values of 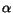 in the range of [0.8, 0.9] seemed typical, and so we assumed that
these values would be appropriate in our setting as well. To our
surprise, the effectiveness of the algorithm increased as the
smoothing parameter
in the range of [0.8, 0.9] seemed typical, and so we assumed that
these values would be appropriate in our setting as well. To our
surprise, the effectiveness of the algorithm increased as the
smoothing parameter 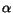 dropped
toward 0.8, and so we continued to examine its performance as we
smoothed the distribution even more. Figure
dropped
toward 0.8, and so we continued to examine its performance as we
smoothed the distribution even more. Figure ![[*]](p432-novak-crossref.png) shows the results for
word-level features; smoothing with
shows the results for
word-level features; smoothing with
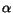 = 0.02 is optimal. Thus,
the most effective technique for smoothing a distribution in our
setting is to replace 98% of it with the generic background
distribution!
= 0.02 is optimal. Thus,
the most effective technique for smoothing a distribution in our
setting is to replace 98% of it with the generic background
distribution!
The reason is the following. Due to the Zipf law on word usage
in natural language [24,23],
each alias of an author will use many words that the other alias
does not use. Each such word use in a naively smoothed distribution
of large 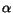 will contribute a term of
will contribute a term of
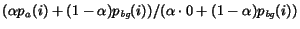 to the measure; this term will be large as
to the measure; this term will be large as 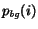 is tiny for such an infrequent term. Thus, if a
particular alias used 17 highly infrequent terms, the most similar
author will be the one who used as many of the 17 as possible, and
normal differences in the frequencies of other terms would be
swamped by this factor. By smoothing heavily, we allow the more
frequent terms to contribute more strongly to the overall
measure.
is tiny for such an infrequent term. Thus, if a
particular alias used 17 highly infrequent terms, the most similar
author will be the one who used as many of the 17 as possible, and
normal differences in the frequencies of other terms would be
swamped by this factor. By smoothing heavily, we allow the more
frequent terms to contribute more strongly to the overall
measure.
Figure: Evaluation of
Smoothing Parameter 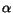 .
.
|
|
5 Clustering Algorithms
Having explored similarity measures, we now turn to clustering
algorithms that make use of the entire family of directed
similarities between aliases in order to determine meaningful
clusters of aliases.
Given a set of aliases A, we define a clustering
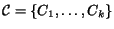 over the
aliases as any partition of the elements of A.2 We
define the ``good'' clustering
over the
aliases as any partition of the elements of A.2 We
define the ``good'' clustering  to
be the correct clustering of the aliases. We define all aliases
within the same cluster of
to
be the correct clustering of the aliases. We define all aliases
within the same cluster of  to
be siblings. For an alias a
to
be siblings. For an alias a 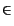 A we define c(a) to be the cluster
of a in
A we define c(a) to be the cluster
of a in  , and
g(a) to be the cluster of a in
, and
g(a) to be the cluster of a in  .
.
Our goal is to develop clustering algorithms; therefore settling
on a measure to evaluate the quality of such an algorithm is of
paramount importance. At its heart, such a measure must compare our
proposed clustering to the correct one. However, there is no
consensus on a single measure for this task, so we must spend some
care in developing the correct framework.
Numerous measures have been proposed to compare clusterings,
based typically on comparing how many pairs of objects are
clustered together or apart by both clusterings, or by comparing
pairs of clusters, or by adopting measures from information theory.
The cleanest formulation of which we are aware is given by
Meila [12], who proposes
addressing many of the concerns with the above methods using a new
measure called the Variation of Information (VI). Let
H and I be the standard entropy and mutual
information measures for distribution. Then for two clusterings
 and
and  , the VI is defined as follows:
, the VI is defined as follows:
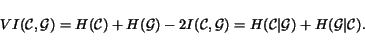
Some useful properties of this measure are:
- VI is a metric
- VI is scale-invariant in the sense that each point can be
doubled without changing the measure
- VI is linear in the sense that the VIs computed on induced
clusterings of subsets of the points can be combined in the final
VI
- The value of VI is bounded above by the logarithm of the number
of items.
Thus, VI is an attractive approach to measuring distance between
clusterings, and we adopt it as such. However, the values of VI are
difficult to interpret, so we would like to preserve the properties
of the measure while allowing the reader to get a better feel for
the results. We observe that a high-quality clustering has two
properties:
- It places siblings in the same cluster
- It places non-siblings in different clusters.
An algorithm can perform well on the first measure by placing
all aliases in the same huge cluster, or can perform well on the
second measure by placing each alias in a distinct cluster. We seek
algorithms that simultaneously perform well on both measures. We
therefore adopt the following definitions. By analogy with the
field of information retrieval, we define the precision
P of a clustering to be the quality of the clustering with
respect to property 1, as follows:
![$P({\cc }) = \sum_{a\in A} \Pr_{b\in c(a)}[g(b) = g(a)]$](p432-novak-img25.png) .
Similarly, we define the recall R of a clustering to
be the quality of the clustering with respect to property 2, as
follows:
.
Similarly, we define the recall R of a clustering to
be the quality of the clustering with respect to property 2, as
follows:
![$R({\cc }) = \sum_{a\in A} \Pr_{b\in g(a)}[c(b) = c(a)]$](p432-novak-img27.png) .
Thus, precision captures the notion that the members of a's
cluster are siblings, while recall captures the notion that the
siblings of a are in the same cluster as a.
.
Thus, precision captures the notion that the members of a's
cluster are siblings, while recall captures the notion that the
siblings of a are in the same cluster as a.
While these two figures of merit share intuition with the
measures from information retrieval, they may behave quite
differently. Most importantly, precision and recall in the context
of a clustering are inherently duals of one another in the sense
that swapping  and
and  swaps the precision and recall values. Since our
context always includes a correct clustering and an algorithmic
clustering, we can use the terms with clarity; in general, though,
they might more accurately be called the 1-recall (recall of
tex2html_wrap_inlineC with respect to tex2html_wrap_inlineG) and
the 2-recall (recall of tex2html_wrap_inlineG with respect to
tex2html_wrap_inlineC), where the i-recall is the (1 -
i)-precision.
swaps the precision and recall values. Since our
context always includes a correct clustering and an algorithmic
clustering, we can use the terms with clarity; in general, though,
they might more accurately be called the 1-recall (recall of
tex2html_wrap_inlineC with respect to tex2html_wrap_inlineG) and
the 2-recall (recall of tex2html_wrap_inlineG with respect to
tex2html_wrap_inlineC), where the i-recall is the (1 -
i)-precision.
Finally, again following the terminology of information
retrieval, we define the F-measure of a clustering
 as
F =
as
F = 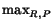 2RP/(R + P), where
R and P are recall and precision.
2RP/(R + P), where
R and P are recall and precision.
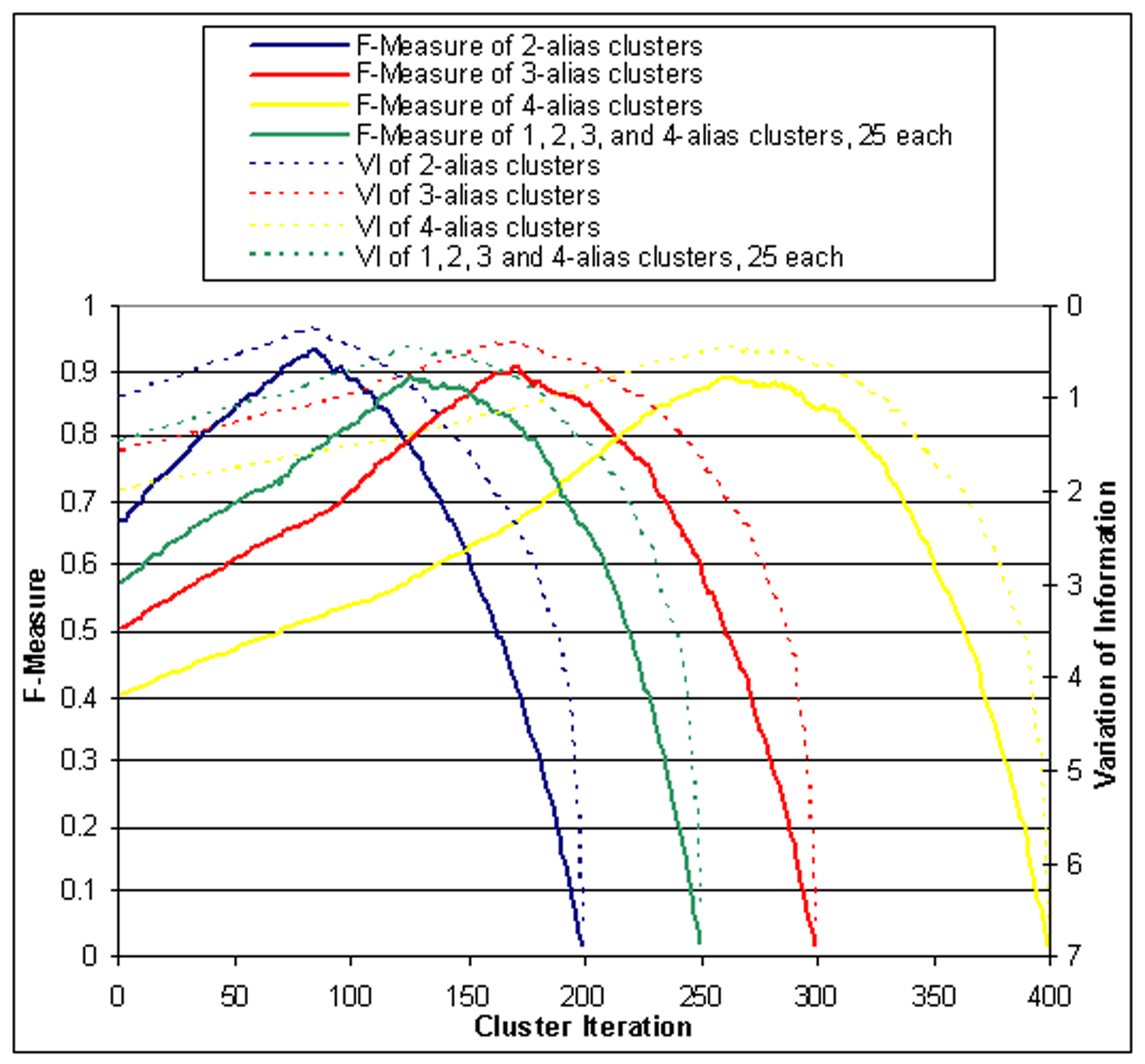
In Figure ![[*]](p432-novak-crossref.png) we show in solid lines
the F-measure for a number of experiments, and in dotted lines, the
VI. The four experiments are described in detail below, but
briefly, they cover domains in which the correct number of aliases
per cluster is exactly 2, 3, or 4, or a mix of values between 1 and
4. The x axis measures the number of merge operations the
clustering algorithm has performed, and the y axis shows the
F-measure and VI of the resulting clustering--the scale for
F-measure is shown on the left and for VI is shown on the right. As
the figure shows, in all cases, the F-measure and the VI track
quite closely over the entire range of number of merges performed
by the algorithm. Thus, we conclude that F-measure captures the
same quality indication as VI for our domain of interest.
Henceforth, for clarity, we will adopt precision, recall and
F-measure as appropriate for graphing results.
we show in solid lines
the F-measure for a number of experiments, and in dotted lines, the
VI. The four experiments are described in detail below, but
briefly, they cover domains in which the correct number of aliases
per cluster is exactly 2, 3, or 4, or a mix of values between 1 and
4. The x axis measures the number of merge operations the
clustering algorithm has performed, and the y axis shows the
F-measure and VI of the resulting clustering--the scale for
F-measure is shown on the left and for VI is shown on the right. As
the figure shows, in all cases, the F-measure and the VI track
quite closely over the entire range of number of merges performed
by the algorithm. Thus, we conclude that F-measure captures the
same quality indication as VI for our domain of interest.
Henceforth, for clarity, we will adopt precision, recall and
F-measure as appropriate for graphing results.
Figure: VI versus
F-measure for Clusterings.
|
|
Having established the measures we will use to evaluate our
success, we now move to a limited variant of the clustering problem
in which all clusters in the ground truth have size 2. We introduce
the ``Mutual Ranking'' method for clustering, which we will later
extend to a more general framework.
The clustering proceeds as follows. We are given a set of
aliases A and a directed similarity measure
Sim(a, b) as defined in Section ![[*]](p432-novak-crossref.png) ; the measure is larger (i.e.,
more similar) if the text of a could have been produced by
the author of b. We define r(a, b) to
be the rank of b in the sorted list of
Sim(a, . ); thus,
r(a, b) = 1 if and only if b is the
most likely author (other than a) to have produced the text
of a. Thus,
r(a, . ) is a permutation of
{c
; the measure is larger (i.e.,
more similar) if the text of a could have been produced by
the author of b. We define r(a, b) to
be the rank of b in the sorted list of
Sim(a, . ); thus,
r(a, b) = 1 if and only if b is the
most likely author (other than a) to have produced the text
of a. Thus,
r(a, . ) is a permutation of
{c 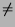 a| c
a| c
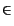 A}. Mutual ranking
iteratively pairs up elements of A greedily according to the
measure
r(a, b) + r(b, a).
A}. Mutual ranking
iteratively pairs up elements of A greedily according to the
measure
r(a, b) + r(b, a).
To benchmark this algorithm, we employed the same test set used
to evaluate our different feature sets. Recall that we extracted
100 aliases from the Laci Peterson board who produced at least 100
articles, and split them into 200 sub-aliases of 50 posts each,
broken at random. We then extracted features using each of our four
different feature sets, and set
Sim = SimMLE. We applied 100 steps of
mutual ranking, and then measured how many of the resulting 100
clusters were ``correct'' in that they contained two sub-aliases of
the same alias. The results are as follows:
| Features |
words |
misspells |
punctuation |
| Correct Clusters |
91 |
66 |
12 |
Figure ![[*]](p432-novak-crossref.png) shows how the precision and recall of the mutual ranking method on
this benchmark change as the algorithm clusters more and more
aliases. The ``sweet spot'' of the curve represents the 91 correct
clusters shown in the table.
shows how the precision and recall of the mutual ranking method on
this benchmark change as the algorithm clusters more and more
aliases. The ``sweet spot'' of the curve represents the 91 correct
clusters shown in the table.
Figure: Clustering Using
Mutual Ranking.
|
|
We now extend the mutual ranking framework to the general
clustering problem. We define an interactive scheme for clustering
aliases. The scheme, which we call greedy cohesion, is given
by the following pseudo-code:
Let
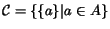 be the ``current clustering''
be the ``current clustering''
Until stopping_condition(C):
Pick
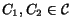 to minimize cohesion(
C1
to minimize cohesion(
C1 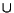 C2)
C2)
Replace C1 and C2 in  with
C1
with
C1 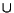 C2
C2
The measure depends on the definition of the cohesion of a set
of aliases; this is the mutual pairwise average ranking, or more
formally:
cohesion(
C') =
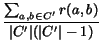
Before we consider the stopping condition, we can evaluate how
well the scheme chooses clusters to merge. We develop a number of
benchmarks for this evaluation, as referenced in our discussion of
clustering measures. The benchmarks are:
- Exactly 2, 3, or 4 aliases per cluster: For these three
benchmark sets we consider authors who have produced 100, 150, or
200 posts respectively, and from these authors take the appropriate
number of 50-post subsets.
- Mixed: This benchmark contains 25 clusters each of size 1, 2,
3, and 4.
- Exponentially decaying with factor
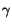 = 0.2 or
= 0.2 or
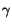 = 0.5: These two
benchmarks contain
100(1 -
= 0.5: These two
benchmarks contain
100(1 - 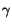 )i clusters of
size i, for
i
)i clusters of
size i, for
i 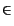 [1..4].
[1..4].
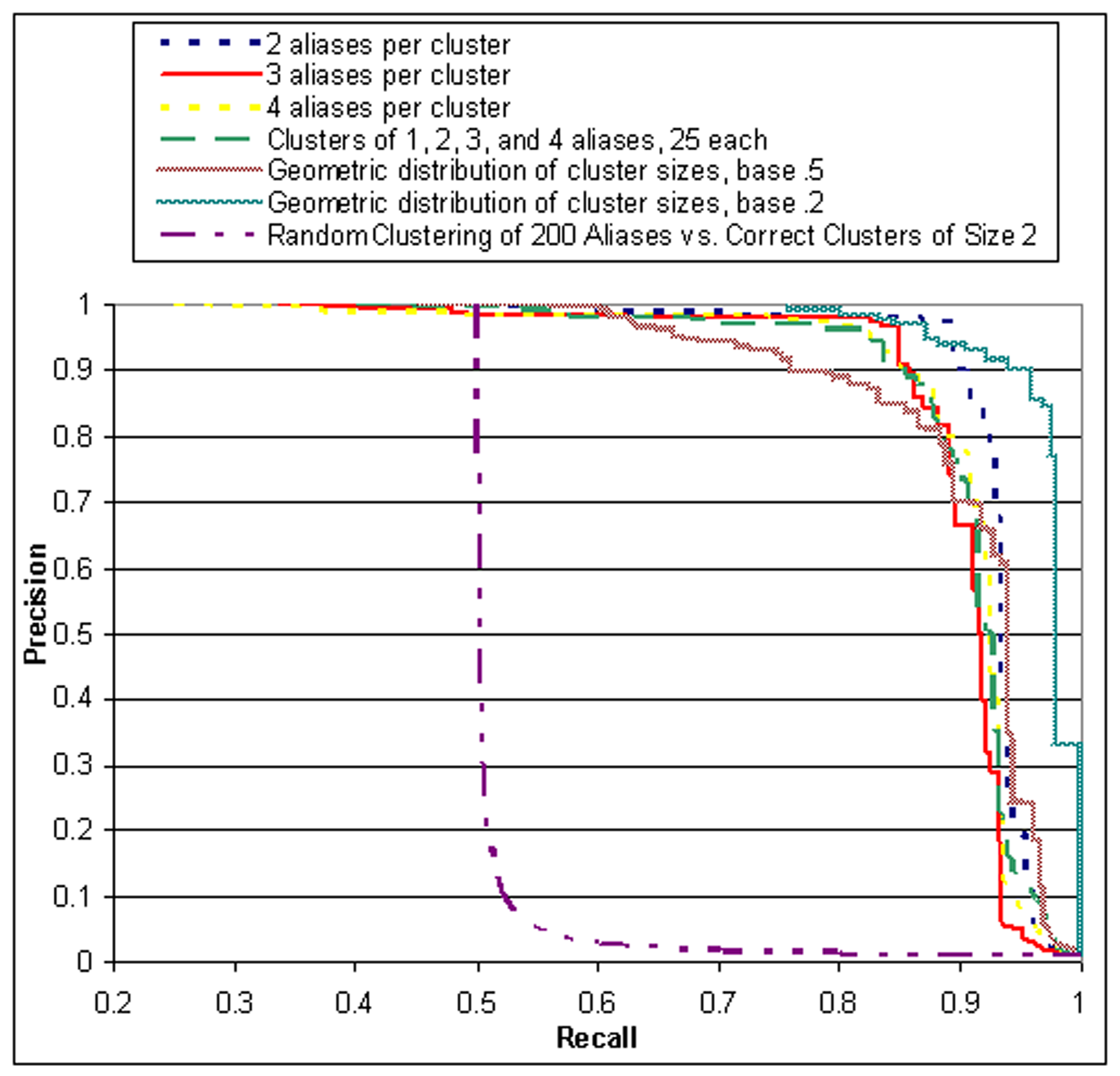
The results are shown in Figure ![[*]](p432-novak-crossref.png) , and the F-measures for
the optimal stopping points are shown in Table
, and the F-measures for
the optimal stopping points are shown in Table ![[*]](p432-novak-crossref.png) . As the figure shows,
for both large clusters and highly skewed clusters, the algorithm
performs quite well. Even for the extreme case of 400 authors and 4
aliases per cluster, the F-measure is still in excess of 0.88.
. As the figure shows,
for both large clusters and highly skewed clusters, the algorithm
performs quite well. Even for the extreme case of 400 authors and 4
aliases per cluster, the F-measure is still in excess of 0.88.
The precision-recall curves we have shown appear reasonable, but
how are we to know that any random clustering scheme would not
perform as well? We perform the following experiment: given a
correct cluster size (for instance, 2), we allow a random
clustering algorithm to know the correct size, and to choose a
random clustering in which each cluster has size exactly 2. We have
added the expected precision/recall of this scheme in Figure
![[*]](p432-novak-crossref.png) to compare it
with the actual algorithm. As the figure shows, the recall begins
at 0.5 because each singleton cluster contains 1/2 of the siblings.
However, until precision has dropped below 0.1, there is no visible
improvement in recall--the number of cluster choices is too large,
and as we would expect, the scheme performs horribly. Thus, any
scheme that manages to move away from the convex form of the random
algorithm is gaining some traction in identifying the correct
clusters.
to compare it
with the actual algorithm. As the figure shows, the recall begins
at 0.5 because each singleton cluster contains 1/2 of the siblings.
However, until precision has dropped below 0.1, there is no visible
improvement in recall--the number of cluster choices is too large,
and as we would expect, the scheme performs horribly. Thus, any
scheme that manages to move away from the convex form of the random
algorithm is gaining some traction in identifying the correct
clusters.
There are many other possible schemes to evaluate the next best
cluster merge. A natural idea is to replace cohesion with
inter-cluster distance (ICD), and pick the pair of clusters that
minimize the inter-cluster distance. ICD is defined as follows:
ICD(
C,
C') =
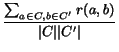
.
We evaluated both schemes, and found that each produced similar
results.
The agglomerative clustering algorithm defined above can
continue merging until there is only one cluster left; this will
improve recall at the cost of precision. We must devise a condition
the algorithm can apply to terminate merging. We begin with two
observations:
Observation 1 If a clustering has k clusters
of size s then the cohesion of any given cluster is no
smaller than s/2.
Proof: Each a in the cluster can rank only 1 element first,
one element second, and so on; its average rank will be
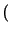
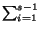 i
i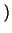 /(s - 1) =
s/2. Likewise for all elements.
/(s - 1) =
s/2. Likewise for all elements.
Observation 2 If a clustering has k clusters
whose average size is s, the average cohesion across all
clusters cannot be less than s/2.
Proof: By induction.
Thus, we adopt the following stopping condition. The algorithm
stops when it cannot find a merge whose cohesion is within twice
the best possible. Formally then, given a clustering problem with |
A| = n that has run for t steps, continue if
and only if the best attainable cohesion is no more than
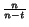
 .
.
Table ![[*]](p432-novak-crossref.png) shows the
results of this stopping condition.
shows the
results of this stopping condition.
Table: Evaluation of Stopping
Condition.
| |
Using Stopping Condition |
Optimal |
| Aliases per Cluster |
F-measure |
Iterations |
F-measure |
Iterations |
| 2 |
.915 |
.89 |
.929 |
85 |
| 3 |
.899 |
166 |
.901 |
172 |
| 4 |
.873 |
253 |
.888 |
261 |
| Mixed |
.888 |
124 |
.890 |
125 |
| Geo 0.2 |
.904 |
48 |
.929 |
37 |
| Geo 0.5 |
.818 |
99 |
.843 |
135 |
|
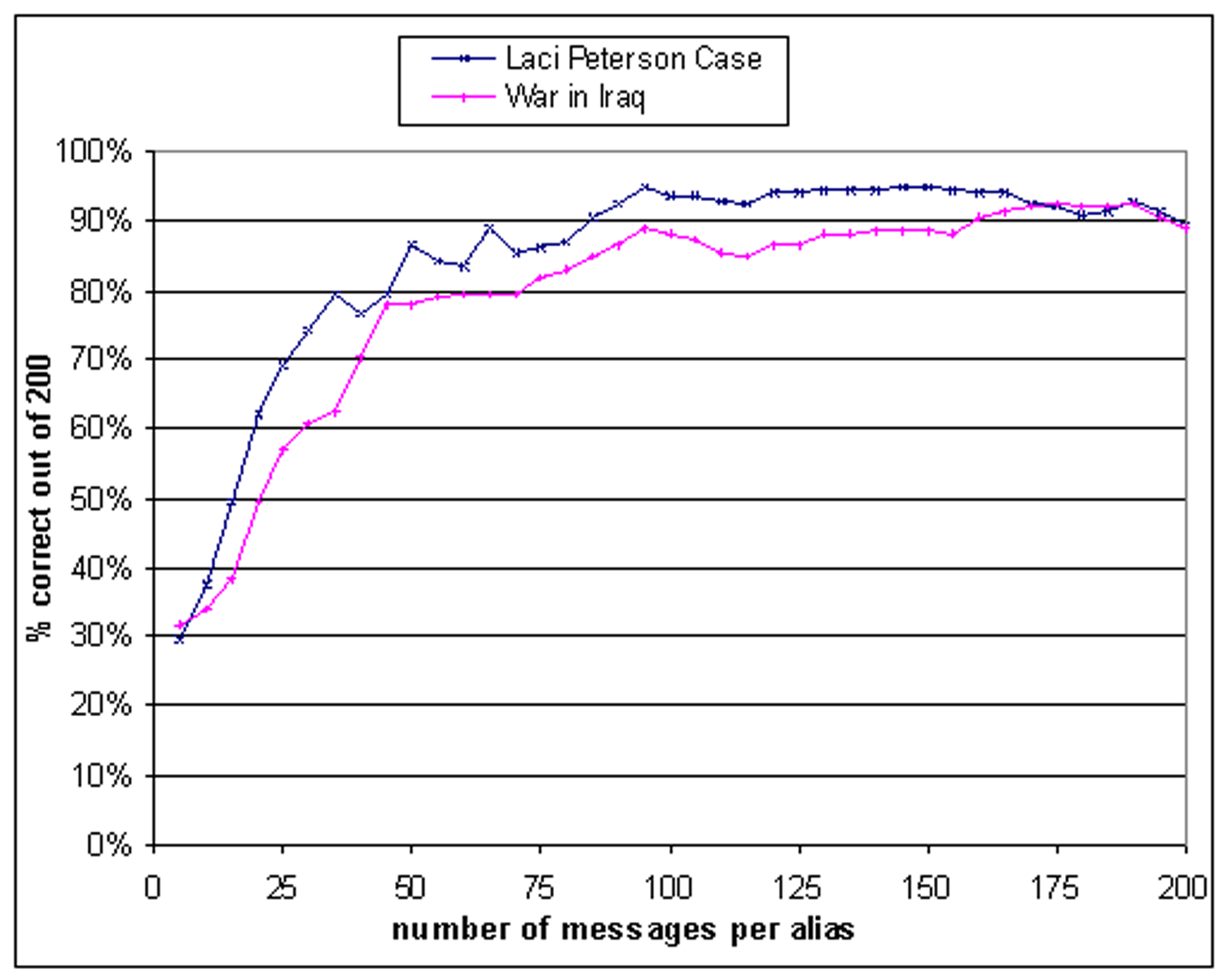
Results using different sized data sets are shown in Figure
![[*]](p432-novak-crossref.png) . The figure
again considers the running benchmark example of splitting the
posts of 100 users into 200 aliases and attempting to re-group. The
y axis plots probability of ranking the correct sub-alias
top out of 199 candidates. As the figure shows, at 50 messages per
alias the results become quite strong, as we have seen before, and
as we move toward 100 or 125 messages, we sometimes attain
probabilities of correct ranking in excess of 95%. The clustering
algorithm typically improves on this probability noticeably.
. The figure
again considers the running benchmark example of splitting the
posts of 100 users into 200 aliases and attempting to re-group. The
y axis plots probability of ranking the correct sub-alias
top out of 199 candidates. As the figure shows, at 50 messages per
alias the results become quite strong, as we have seen before, and
as we move toward 100 or 125 messages, we sometimes attain
probabilities of correct ranking in excess of 95%. The clustering
algorithm typically improves on this probability noticeably.
Figure: Evaluation of
different sized data sets
|
|
6 Real World Data
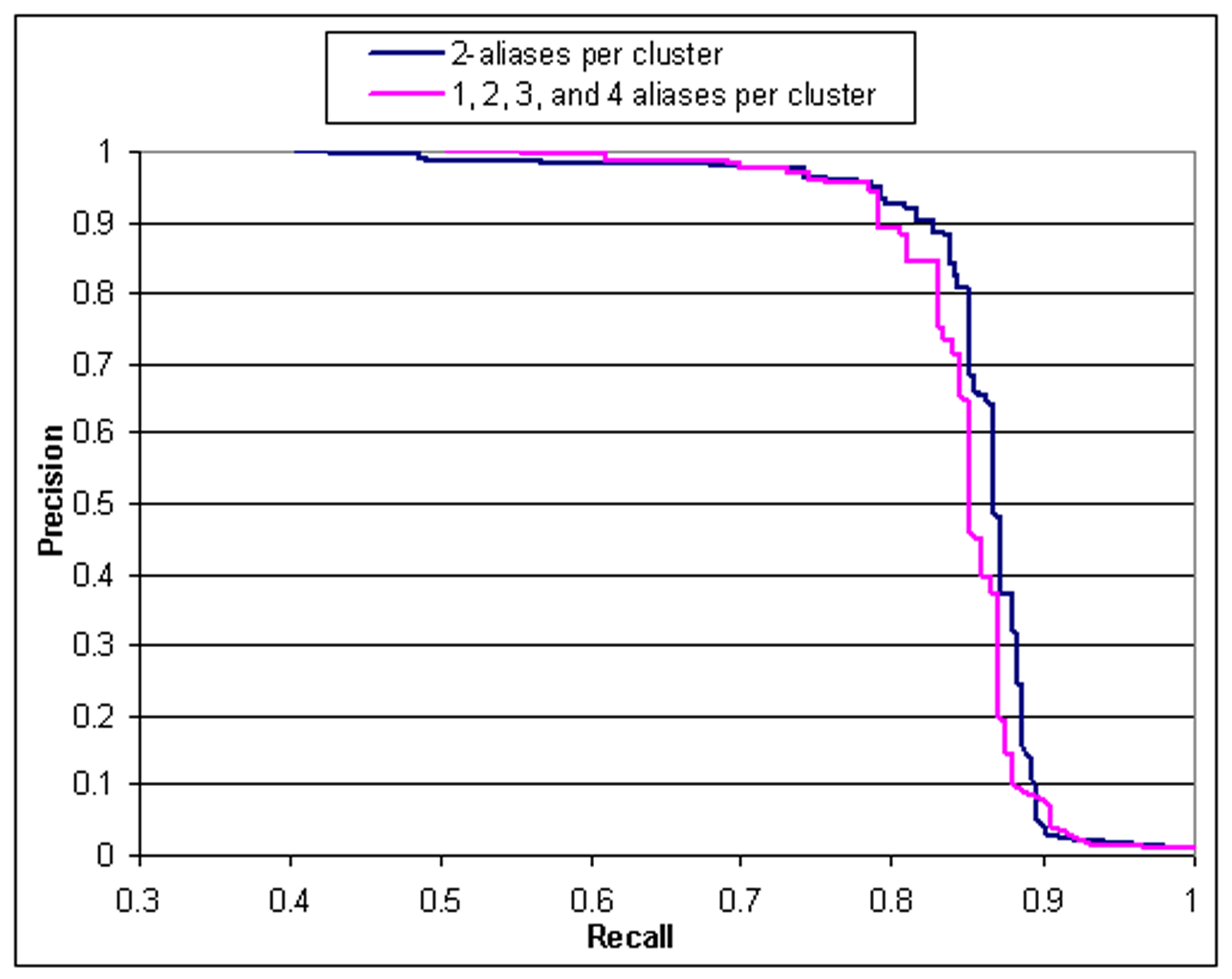
Figure: Evaluation of
clustering multi-topic data
|
|
We now apply our clustering system in two real world
experiments: clustering aliases using postings across multiple
topics, and discovering non-synthetic multiple-aliases within a
message board.
Postings on multiple topics present an additional challenge to
clustering aliases. To investigate this problem we set up the
following experiments:
- As before, we split the postings for 100 users into 200
sub-aliases. However, for this experiment, the postings for each
sub-alias consisted of 25 postings from the Laci Peterson board,
and 25 from the War in Iraq message board. We then tried to
re-group the sub-aliases using our clustering algorithm.
- Using postings from 100 users, we created 25 clusters each of
size 1, 2, 3, and 4 with half of each clusters' postings from the
Laci Peterson board, and half from the War in Iraq board. Again we
tried to re-group.
Since our algorithm depends on a user's vocabulary being
consistent across postings, messages from the same user on
different topics tend not be clustered together. To get around this
problem, we devised the following scheme to discount vocabulary
specific to a particular message board topic:
Let t(w, b) be the tf-idf score for word
w within message board b. Remove any word w
where
| log[t(w, b)] -
log[t(w, a)]| > 2. For each
remaining word w in message board b, if
t(w, a) < t(w, b),
multiply each user's probability of using w by
t(w, a)/t(w, b).
After applying the above, we then used our Mutual Ranking method
as previously described. Results from these experiments are shown
in Figure ![[*]](p432-novak-crossref.png) .
.
As a final experiment, we applied our anti-aliasing system to a
dataset without synthetically derived aliases. Using a fresh set of
postings from several topics, we ran our clustering algorithm to
identify users who were writing under multiple aliases. To evaluate
our recall and precision, we scanned the postings for common
patterns and clues that one alias was, or was not, the same user.
We quickly realized that a complete analysis was infeasible,
especially in identifying which clusters were missing. We opted
instead for evaluating the accuracy of a subset of the enumerated
clusters.
Using our system, we clustered 400 aliases on the Laci Peterson
message board with between 10 and 200 postings each. Our algorithm
resulted in 339 clusters, 56 of size two, one of size three, and
one of size four. Seven of the clusters appeared to be correct
based on the aliases alone, for example: ``deli princess'' and
``deli princess2'' or ``Anita Mann'' and ``Anita Newman''. These
seem to be cases where the user is not attempting to disguise the
use of multiple aliases. We then evaluated a sample of 12
non-obvious clusters for accuracy. By our judgment, 9 were correct,
2 were incorrect, and on one cluster we remained undecided.
As an example of the criteria we used in our evaluation, we
present the following as evidence that Amadine and ButlerDidIt were
indeed two aliases for the same user that were discovered by our
algorithms:
- Both use ``(s)'' excessively. Examples:
- Amadine:
``Roxie, thanks very much for the link .... I've bookmarked it
and I'm going to purchase the book(s) as soon as I get the
chance.''
- ButlerDidIt: ``Scott could have called someone in his family
(who live in San Diego) - his brother(s) or his father - and that
person(s) could have met him halfway, transferred the body and
disposed of it somewhere closer to San Diego - far away from
Modesto.''
- Similar vocabulary. Examples:
- Amadine:
``Scott's subsequent behavior nailed the lid shut for
me''
``Now let's look at another scenario...''
- ButlerDidIt:
``It's hard to imagine such a conversation (and subsequent plan)
playing out''
``And in another scenario...''
- Both use numbered bullets. Examples:
- Amadine:
``I have a few concerns regarding Greta ...
1. Why does she have all these "teasers" to get viewers?
2. Why does she only have defense lawyers?
3. Why does the Fox Network think she's so great?
4. Why does she irritate me so much?''
- ButlerDidIt:
``I've been wondering if anybody knows...
1. If you were trying to weight a body down so it wouldn't float to
the top, how much weight in proportion to the body would you need
to make sure that it stayed under?...
2. As for prevention it from floating to the surface, if it doesn't
go all the way to the bottom, is it likely (provided the weights
stay intact) to float at some level below the surface...?
3. Assuming you had enough weight to get the body to the bottom of
the ocean (or marina, lake, etc.) floor, is it still likely to get
completely consumed by ocean life...``
Some of the criteria we used would be taken into account by our
algorithm. For example, AvidReader and BoredInMichigan both dropped
apostrophes in conjunctions, as in ``dont'', ``didnt'', and
``wasnt''. They also both used the expression ``he, he, he''
excessivley.
- AvidReader: ``He He He...sorry I have to intervene
here...''
- BoredInMichigan: ``He He He...Its working''
Other criteria we used were more subjective. For example
AuroraBorealis and dalmationdoggie made spelling mistakes we felt
were similar:
- AuroraBorealis: embarrassing
- dalmationdoggie: interested, allot
Our analysis uncovered a drawback to our technique. Users who
engage in an intense discussion on a slightly off-topic area, or
who focus intently on the same side-topic for a series of posts,
tend to get grouped together. One example is ColdWater and
ClaraBella who are clustered together by our algorithm. ColdWater
is the moderator for a particular thread; the bulk of this user's
postings are answers to technical questions about how to use the
software. ClaraBella's posts also address the technical aspects of
the software as she answers questions posed by a new user of the
message board. Addressing this anomaly appears to require a classic
combination of traditional text classification methods with ours:
while the former would focus on ``content-rich'' features that
focused on the topic(s) of discussion, our methods would focus on
features that are symptoms of a given author.
7 Conclusion
In this paper, we have shown that matching aliases to authors
with accuracy in excess of 90% is practically feasible in online
environments. Our techniques are most effective when two aliases of
the same author post on the same bulletin board--there is
significant cause for concern from a privacy perspective in this
arena. Across bulletin boards, or even across sites, however, as
the number of posts grows our techniques appear able to uncover
aliases with an effectiveness that leads us to suggest that
compromise of privacy is a very real possibility.
We have two areas of open problems. The first relates to the
algorithm: how can it be improved, and can the techniques used for
larger number of authors be applied meaningfully in the stylometric
problem domain.
Our second area of open problems is broader but perhaps more
critical. Are there meaningful countermeasures for techniques like
ours? In particular, can users be given tools or training to make
them less susceptible to such attacks? Our algorithms at present
have not been optimized to run at web scale, but we have no reason
to believe that scale alone will provide an adequate barrier. Our
primary suggestion to users is to avoid behaviors that might allow
algorithms to make rapid progress in bringing aliases together.
Such behaviors would include posting on the same board, using a
similar signature file, or mentioning the same people, places, or
things. We would recommend avoiding characteristic language, but
this is almost impossible to implement. Once a candidate alias has
been discovered by a more advanced form of our system, techniques
like correlation of posting times and analysis of evolution of
discourse and vocabulary could be quite powerful, so in some ways
there is safety in keeping personas apart.
But short of making it more difficult for programs to identify
aliases, we do not have a suggestion for countering this type of
technique, for users who will be entering non-trivial amounts of
text under multiple personas which should be kept separate.
- 1
- S. Argamon, M. Koppel, and G. Avneri.
Routing documents according to style.
In Proceedings of First International Workshop on Innovative
Information Systems, 1998.
- 2
- B. Brainerd.
The computer in statistical studies of William Shakespeare.
Computer Studies in the Humanities and Verbal Behavior,
4(1), 1973.
- 3
- David Chaum.
Untraceable electronic mail.
Communications of the ACM, 24(2):84-88, February,
1981.
- 4
- David Chaum.
Security without identification: Transaction systems to make big
brother obsolete.
Communications of the ACM, 28(10):1030-1044, October,
1985.
- 5
- Olivier Y. de Vel, A. Anderson, M. Corney, and George M.
Mohay.
Mining email content for author identification forensics.
SIGMOD Record, 30(4):55-64, 2001.
- 6
- Joachim Diederich, Jörg Kindermann, Edda Leopold, and
Gerhard Paass.
Authorship attribution with support vector machines.
- 7
- W. Frakes and R. Baeza-Yates.
Information Retrieval: Data Structures and
Algorithms.
Prentice Hall, 1992.
- 8
- E. Friedman and P. Resnick.
The social cost of cheap pseudonyms.
Journal of Economics and Management Strategy,
10(2):173-199, 2001.
- 9
- Eran Gabber, Phillip B. Gibbons, David M. Kristol, Yossi
Matias, and Alain Mayer.
On secure and pseudonymous client-relationships with multiple
servers.
ACM Transactions on Information and System Security,
2(4):390-415, 1999.
- 10
- I. Krsul and E. H. Spafford.
Authorship analysis: Identifying the author of a program.
In Proc. 18th NIST-NCSC National Information Systems Security
Conference, pages 514-524, 1995.
- 11
- Hang Li and Naoki Abe.
Clustering words with the MDL principle.
In COLING96, pages 4-9, 1996.
- 12
- M. Meila.
Comparing clusterings.
Technical Report 418, UW Statistics Department, 2002.
- 13
- F. Mosteller and D. Wallace.
Inference and Disputed Authorship: The Federalist.
Addison-Wesley, 1964.
- 14
- Josyula R. Rao and Pankaj Rohatgi.
Can pseudonymity really guarantee privacy?
In Proceedings of the Ninth USENIX Security Symposium,
pages 85-96. USENIX, August 2000.
- 15
- Edie Rasmussen.
Clustering Algorithms, chapter 16.
Prentice Hall, 1992.
- 16
- M. Reed and P. Syverson.
Onion routing.
In Proceedings of AIPA, 1999.
- 17
- M. Reiter and A. Rubin.
Anonymous web transactions with crowds.
Communications of the ACM, 42(2):32-38, 1999.
- 18
- Zero Knowledge Systems, 2000.
- 19
- Yuta Tsuboi and Yuji Matsumoto.
Authorship identification for heterogeneous documents.
Master's thesis, Nara Institute of Science and Technology,
2002.
- 20
- Ellen M. Voorhees.
The effectiveness and efficiency of agglomerative hierarchic
clustering in document retrieval.
PhD thesis, Cornell University, 1986.
- 21
- P. Willet.
Recent trends in hierarchic document clustering: a critical
review.
Information Processing and Manaagement, 24(5):577-597,
1988.
- 22
- C. Williams.
Mendenhall's studies of word-length distribution in the works of
Shakespeare and Bacon.
Biometrika, 62:207-212, 1975.
- 23
- G. U. Yule.
Statistical Study of Literary Vocabulary.
Cambridge University Press, 1944.
- 24
- G. K. Zipf.
Human Behavior and the Principle of Least Effort.
Addison-Wesley, 1949.
Footnotes
- 1
- Some examples might include: and, but, which, that, might,
this, very, however, and punctuation symbols.
- 2
- A partition has two properties: every alias belongs to at least
one cluster, and no alias belongs to multiple clusters.
![[*]](p432-novak-crossref.png) by covering related work. In
Section
by covering related work. In
Section ![[*]](p432-novak-crossref.png) we
develop our similarity measure capturing the likelihood that each
author in the system generated a particular collection of text.
Next, in Section
we
develop our similarity measure capturing the likelihood that each
author in the system generated a particular collection of text.
Next, in Section ![[*]](p432-novak-crossref.png) we describe combining
the output of the similarity measure into a clustering of aliases
representing the underlying individuals. In Section
we describe combining
the output of the similarity measure into a clustering of aliases
representing the underlying individuals. In Section ![[*]](p432-novak-crossref.png) , we describe a case study
moving from our analytical domain into a real world bulletin board
with no planted clusters.
, we describe a case study
moving from our analytical domain into a real world bulletin board
with no planted clusters.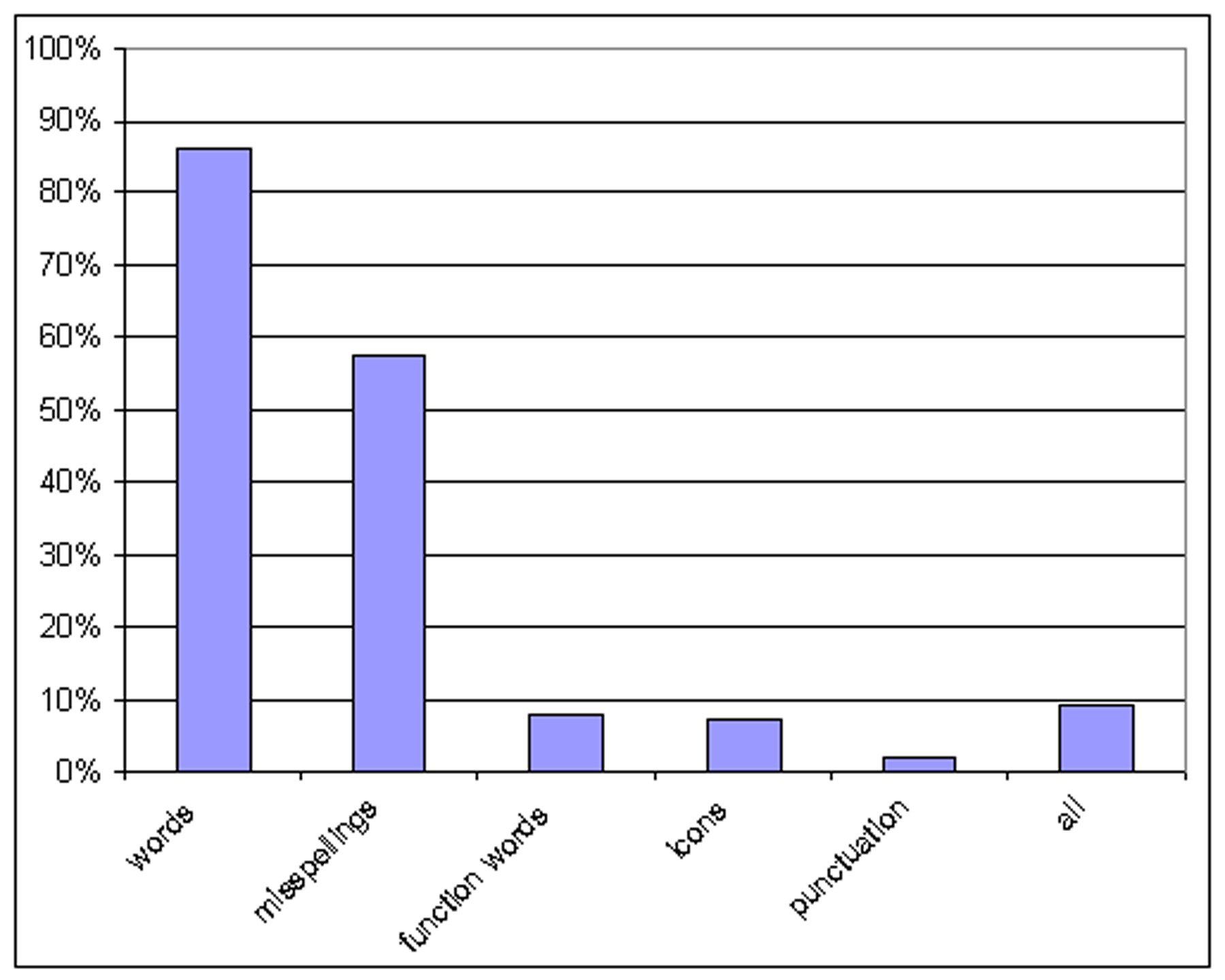
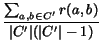
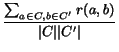 .
.