Abstract: The web harbors a large number of communities -- groups of content-creators sharing a common interest -- each of which manifests itself as a set of interlinked web pages. Newgroups and commercial web directories together contain of the order of 20000 such communities; our particular interest here is on emerging communities -- those that have little or no representation in such fora. The subject of this paper is the systematic enumeration of over 100,000 such emerging communities from a web crawl: we call our process trawling. We motivate a graph-theoretic approach to locating such communities, and describe the algorithms, and the algorithmic engineering necessary to find structures that subscribe to this notion, the challenges in handling such a huge data set, and the results of our experiment.
Keywords: web mining, communities, trawling, link analysis
The web has several thousand well-known, explicitly-defined communities -- groups of individuals who share a common interest, together with the web pages most popular amongst them. Consider for instance, the community of web users interested in Porsche Boxster cars. There are several explicitly-gathered resource collections (e.g., Yahoo's Recreation: Automotive: Makes and Models: Porsche: Boxster) devoted to the Boxster. Most of these communities manifest themselves as newsgroups, webrings, or as resource collections in directories such as Yahoo! and Infoseek, or as homesteads on Geocities. Other examples include popular topics such as "Major League Baseball," or the somewhat less visible community of "Prepaid phone card collectors". The explicit nature of these communities makes them easy to find -- it is simply a matter of visiting the appropriate portal or newsgroup. We estimate that there are around twenty thousand such explicitly-defined communities on the web today.
The results in this paper suggest that the distributed, almost chaotic nature of content-creation on the web has resulted in many more implicitly-defined communities. Such implicitly-defined communities often focus on a level of detail that is typically far too fine to attract the current interest (and resources) of large portals to develop long lists of resource pages for them. Viewed another way, the methods developed below identify web communities at a far more nascent stage than do systematic and institutionalized ontological efforts. (The following preview of the kinds of communities we extract from the web may underscore this point: the community of Turkish student organizations in the US, the community centered around oil spills off the coast of Japan, or the community of people interested in Japanese pop singer Hekiru Shiina.)
There are at least three reasons for systematically extracting such communities from the web as they emerge. First, these communities provide valuable and possibly the most reliable, timely, and up-to-date information resources for a user interested in them. Second, they represent the sociology of the web: studying them gives insights into the intellectual evolution of the web. Finally, portals identifying and distinguishing between these communities can target advertising at a very precise level.
Since these implicit communities could outnumber the explicit ones by at least an order of magnitude, it appears unlikely that any explicity-defined manual effort can successfully identify and bring order to all of these implicit communities, especially since their number will continue to grow rapidly with the web. Indeed, as we will argue below, such communities sometimes emerge in the web even before the individual participants become aware of their existence. The question is the following: can we automatically recognize and identify communities that will clearly pass under the radar screen of any human ontological effort?
The subject of this paper is the explicit identification of (a large number of) these implicit communities through an analysis of the web graph. We do not use search or resource-gathering algorithms that are asked to find pages on a specified topic. Instead, we scan through a web crawl and identify all instances of graph structures that are indicative signatures of communities. This analysis entails a combination of algorithms and algorithmic engineering aimed at enumerating occurrences of these subgraph signatures on the web. We call this process trawling the web.
In the process of developing the algorithm and system for this process, many insights into the fine structure of the web graph emerge; we report these as well.
Information foraging: The information foraging paradigm was proposed inPirolli, Pitkow, and Rao 96. In their paper, the authors argue that web pages fall into a number of types characterized by their role in helping an information forager find and satisfy his/her information need. The thesis is that recognizing and annotating pages with their type provides a signigicant "value add" to the browsing or foraging experience. The categories they propose are much finer than the hub and authority view taken in Kleinberg 98, and in the Clever project. Their algorithms, however, appear unlikely to scale to sizes that are interesting to us.
The web as a database:
A
view of the web as a semi-structured database has been advanced by many
authors. In particular, LORE, (see Abiteboul et. al. 97)
and WebSQL (see Mendelzon, Mihaila, and Milo 97)
use graph-theoretic and relational views of the web. These views support
a structured query interface to the web (Lorel and WebSQL, respectively)
which is evocative of and similar to SQL. An advantage of this approach
is that many interesting queries, including methods such as HITS, can be
expressed as simple expressions in the very powerful SQL syntax. The associated
disadvantage is that the generality comes with a computational cost which
is prohibitive in our context. Indeed, LORE and WebSQL are but two examples
of projects in this space. Some other examples are W3QS (Konopnicki
and Shmueli 98), WebQuery (Carriere and Kazman
97), Weblog (Lakshmanan, Sadri and Subramanian 96),
and ParaSite (Spertus 97).
Data mining: Traditional data mining research, see for instance Agrawal and Srikant 94, focuses largely on algorithms for inferring association rules and other statistical correlation measures in a given dataset. Our notion of trawling differs from this literature in several ways.
Linkage between these related pages can nevertheless be established by a different phenomenon that occurs repeatedly: co-citation. For instance www.swim.org/church.html, www.kcm.co.kr/search/church/korea.html, and www.cyberkorean.com/church all contain numerous links to Korean churches (these pages were unearthed by our trawling). Co-citation is a concept which originated in the bibliometrics literature (see for instance, White and McCain 89). The main idea is that pages that are related are frequently referenced together. This assertion is even more true on the web where linking is not only indicative of good academic discourse, but is an essential navigational element. In the AT&T/Sprint example, or in the case of IBM and Microsoft, the corporate home pages do not reference each other. On the other hand, these pages are very frequently "co-cited." It is our thesis that co-citation is not just a characteristic of well-developed and explicitly-known communities but an early indicator of newly emerging communities. In other words, we can exploit co-citation in the web graph to extract all communities that have taken shape on the web, even before the participants have realized that they have formed a community.
There is another property that distinguishes references in the web and is of interest to us here. Linkage on the web represents an implicit endorsement of the document pointed to. While each link is not an entirely reliable value judgment, the sum collection of the links are a very reliable and accurate indicator of the quality of the page. Several systems -- e.g., HITS, Google, and Clever -- recognize and exploit this fact for web search. Several major portals also apparently use linkage statics in their ranking functions because, unlike text-only ranking functions, linkage statistics are relatively harder to "spam."
Thus, we are left with the following mathematical version of the intuition we have developed above. Web communities are characterized by dense directed bipartite subgraphs. A bipartite graph is a graph whose node set can be partitioned into two sets, which we denote F and C. Every directed edge in the graph is directed from a node u in F to a node v in C. A bipartite graph is dense if many of the possible edges between F and C are present. Without mathematically pinning down the density, we proceed with the following hypothesis: the dense bipartite graphs that are signatures of web communities contain at least one core, where a core is a complete bipartite subgraph with at least i nodes from F and at least j nodes from C (recall that a complete bipartite graph on node-sets F, C contains all possible edges between a vertex of F and a vertex of C). Note that we deviate from the traditional definition in that we allow edges within F or within C. For the present, we will leave the values i, j unspecified. Thus, the core is a small (i, j)-sized complete bipartite subgraph of the community. We will find a community by finding its core, and then use the core to find the rest of the community. The second step -- finding the community from its core can be done, for instance, by using an algorithm derived from the Clever algorithm. We will not describe this latter step in detail here. We will instead focus the rest of this paper on the more novel aspect, namely algorithms for finding community cores efficiently from the web graph, and the potential pitfalls in this process. Our algorithms make heavy use of many aspects of web structure that emerged as we developed our algorithms and system; we will explain these as we proceed.
We first state here a fact about random bipartite graphs. We then derive from it a less precise hypothesis that, by our hypothesis, applies to web communities (which cannot really be modeled as random graphs). We do this to focus on the qualitative aspects of this imprecise hypothesis rather than its specific quantitative parameterization.
Fact 1: LetB be a random bipartite graph with edges directed from a set L of nodes to a set R of nodes, with m random edges each placed between a vertex of L and a vertex of R uniformly at random. Then there exist i, j that are functions of (|L|, |R|, m) such that with high probability, B contains i nodes from L and j nodes from R forming a complete bipartite subgraph.
The proof is a standard exercise in random graph theory and is omitted; the details spelling out the values of i and j, and "high probability" can be derived easily. For instance, it is easy to show that if |L|=|R|=10 and m=50, then with probability more than 0.99 we will have i and j at least 5. Thus, even though we cannot argue about the distribution of links in a web community, we proceed with the following hypothesis.
Hypothesis 1: A random large enough and dense enough bipartite directed subgraph of the web almost surely has a core.
The most glaring imprecision
in the hypothesis is what is meant by a dense enough and large enough random
bipartite subgraph. Indeed, answering this question precisely will
require developing a random graph model for the web. The second source
of imprecision is the phrase "almost surely." And finally we leave unspecified
the appropriate values of i and j. We state this hypothesis
largely to motivate finding large numbers of web communities by enumerating
all cores in the web graph; we use our experiments below to validate this
approach. Note that a community may have multiple cores, a fact that
emerges in our experiments. Note also that the cores we seek are
directed
-- there is a set of i pages all of which hyperlink to a set of
j
pages, while no assumption is made of links out of the latter set
of j pages. Intuitively, the former are pages created by members
of the community, focusing on what they believe are the most valuable pages
for that community (of which the core contains j). For this
reason we will refer to the i pages that contain the links as fans,
and
the j pages that are referenced as centers
(as in community
centers).
The raw web crawl consisted
of about 1 Terabyte of web data on tape. The data was text-only HTML source
and represented the content of over 200 million web pages, with the average
page containing about 5Kbytes of text. Compared to the current size
of the web,(see Bharat and Broder 98) the volume
of data is significantly smaller. This difference, however, should not
be an impediment to implementing many of our methods on the entire web,
as we will point out below. All our experimentation was done on a single
IBM PC with an Intel 300MHz Pentium II processor, with 512M of memory,
running Linux. The total running time of our experiment was under two weeks.
In our case, however, even approximate mirroring that only preserves most of the links (say 90% of them) can be fatal. A page that is approximately mirrored say three times can produce a very large spurious core, e.g., a (3, k) core where k can be large (here k would be the number of links preserved in all the mirrorings). Even if, say, one in a hundred of our potential fans were approximately duplicated in this fashion, we would have as many spurious communities as real ones.
Consequently, we choose a very aggressive mirror-elimination strategy. The number of shingles we maintain is rather small: only two per page. We also use a relatively small local window (five links) over which to compute the shingles. While these aggressive choices for the shingle algorithm parameters can and probably do result in a few distinct pages being misidentified as mirrors, it detects almost all mirrors and near mirrors reliably. Thus, we are able to effectively deal with the problem posed by near mirrors generating spurious communities.
Of the 24 million pages that
were chosen as potential fans, mirror elimination based on shingling removed
60% of the pages (this refers to the number of potential fans; the number
of potential centers remaining is roughly 30 times the number of potential
fans, at all stages). A natural question would be whether the shingling
strategy was overly aggressive. To convince ourselves of this we examined
by hand a sample of the deleted pages and found that in almost every case,
the deleted page was indeed a mirror page. Indeed we found many of the
duplicates were due to idiosyncrasies in the crawl. For instances, urls
such as http://foo.com/x/y/and http://foo.com/x/y/../y/ (clearly the same)
were treated as distinct. Another problem was the plethora of plagiarized
Yahoo! pages. Many instances of Yahoo! pages had as many as 50 copies.
Here is an instance of four pages in the crawl whose content is almost
the same.
http://www.sacher.com/~schaller/shop/shop_mo.htm
http://www.assoft.co.at/~schaller/shop/shop_mo.htm
http://www.technosert.co.at/~schaller/shop/shop_mo.htm
http://www.der-reitwagen.co.at/~schaller/shop/shop_mo.htm
Even after mirror deletion,
one cannot hope (especially given the constraints of memory hierarchies)
to efficiently enumerate all cores using a classical relational approach
(as, say, an SQL statement in a database, or its web equivalent, WebSQL.)
If n were to denote the number of pages remaining, and i
were the size of the core, this would lead to a running time that grew
roughly as ni, which is prohibitive for any i
larger than 1. It is therefore essential to better exploit the detailed
characteristics of the web graph to prune the data down, eliminating those
potential fans that can be proved not to belong to any community; we begin
describing this process now. Indeed, inferring and understanding
some of these characteristics is a fascinating study of the web graph of
interest in its own right.
This chart includes pages
that have in-degree at most 410. For any integer k larger
than 410, the chance that a page has in-degree k is less than 1
in a million. These unusually popular pages (such as www.yahoo.com
) with many potential fans pointing to them have been excluded.
The chart suggests a simple relation between in-degree values and their
probability densities. Indeed, as can be seen from the remarkably
linear log-log plot, the slope of the curve is close to 1/2. This allows
us to state the following empirical fact.
Empirical fact: The probability that a page has in-degree i is roughly 1/i2.
The precise exponent is slightly
larger than 2. For our purposes however, 2 is close enough. Also, by elementary
probability, we see that the chance that a page has degree at least i
is proportional to 1/i.
However, large and dense bipartite graphs can and do contain many instances of the small cores that we are looking for. This creates an implementation problem: if an algorithm were to list all possible cores in the web graph, then we could be stuck in a situation where most of the cores corresponded to very "high-level" communities (e.g., Physics) and would leave us with a needle-in-the-haystack problem to find and distinguish those that were emerging or new. Pruning by in-degree is a simple method of addressing this potential problem. We delete all pages that are very highly referenced on the web, such as the home pages of web portals (e.g., Yahoo! or Altavista). These pages are presumably referenced for a variety of reasons not having to do with any single emerging community, and hence can safely be eliminated from further consideration. (On the other hand if we were to retain them, we raise the odds of discovering spurious "communities" because pages on various subjects may contain links to these sites just for the creators' convenience.) We therefore eliminate (as potential centers) all pages that have an in-degree greater than a carefully-chosen threshold k. The issue, then, is the particular choice of k.
We posit that pages listed
in a web directory such as Yahoo! are relatively uninteresting from our
point of view. This is because these pages belong to communities that are
already developed and explicitly known. We further note that directory
services listing explicitly-known communities, like Yahoo!, list about
10 Million pages. Let us further approximate by 400 million the order of
magnitude of the number of pages in the web today. Thus, the chance
that a page is already known to be part of an explicitly-known community
is about 1 in 40. From the empirical fact,
such a node would have in-degree 40 or larger. The exact constants turn
out not to be critical; the calculation above shows that the correct value
is around 40. We conservatively set k to 50, and prune all pages
that have in-degree 50 or larger from further consideration as centers.
A critical requirement of
algorithms in this phase is the following. The algorithms must be
implementable as a small number of steps, where in each step the data is
processed in a stream from disk and then stored back after processing onto
disk. Main memory is thus used very carefully. The only other operation
we employ is a sorting of the dataset -- an efficient operation in most
platforms.
Because of this, it becomes necessary to design pruning algorithms that efficiently stream the data between secondary and main memory. Luckily, our iterative pruning process is reducible to sorting repeatedly. We sort the edge list by source, then stream through the data eliminating fans that have low out-degree. We then sort the result by destination and eliminate the centers that have low in-degree. We sort by source again, and then again by destination and so on until we reach a point when only few fans/centers are eliminated in each iteration. In fact it is not necessary to repeatedly sort: it suffices to remember and index in memory all the pruned vertices (or more generally, if in each pass we only pruned as many vertices as we could hold in main memory). We would then have two data sets, containing identical data, except that in one case the edges are sorted by source and in the other they are sorted by destination. We alternately scan over these data sets, identifying and pruning pages that do not meet the in-degree or outdegree threshold. We hold and index the set of vertices being pruned in each iteration in memory. This results in a significant improvement in execution time, because there are only two calls to a sorting routine.
The fact that this form of
pruning can be reduced to a computation on a data stream and sorting is
significant. It would be impossible to do this pruning using a method that
required the indexing of edges by source, by destination, or both. Such
an index would necessarily have to live on disk and accesses to it could
prove to be expensive due to the non-locality of disk access. Designing
a method which streams data efficiently through main memory is relatively
simple in the case of iterative pruning. It is considerably more
challenging when the pruning strategy becomes more sophisticated,
as in the case of inclusion-exclusion pruning, the strategy we describe
next.
The fans (resp. centers) that we choose for inclusion-exclusion pruning are those whose out-degrees (resp. in-degrees) are equal to the threshold j (resp. i). It is relatively easy to check if these nodes are part of any (i, j) core. Consider a fan x with out-degree exactly j, and let N(x) denote the set of centers it points to. Then, x is in an (i, j) core if and only if there are i-1 other fans all pointing to each center in N(x). For small values of i and j and given an index on both fans and centers, we can check this condition quite easily. The computation is simply computing the size of the intersection of j sets and checking if the cardinality is at least i. How can we avoid having two indices in main memory?
First notice that we do not need simultaneous access to both indices. The reason is that we can first eliminate fans with out-degree j and then worry about centers with in-degree i. That is, first, from the edge list sorted by the source id, we detect all the fans with out-degree j. We output for each such fan the set of j centers adjacent to it. We then use an index on the destination id to generate the set of fans pointing to each of the j centers and to compute the intersection of these sets.
A somewhat more careful investigation reveals that all of these intersection computations can be batched, and therefore, we do not require even one index. From a linear scan of the edges sorted by source find fans of out-degree exactly j. For as many of the fans as will fit in memory, index edges sourced at the fan by destination id's. At this stage, we have in memory an index by centers which for each center contains fans adjacent to then which have out-degree exactly j. Clearly this is a much smaller index: it contains only edges that are adjacent to fans of out-degree exactly j.
We will now maintain a set of vertices corresponding to each fan whose edges we have indexed. Recall that each retained fan x is adjacent to exactly j centers. This allows us to consider a "dual" condition equivalent to the condition above.
Fact 2: Let {c1,c2,....,cj} be the centers adjacent to x. Let N(ct) denote the neighborhood of ct, the set of fans that point to ct. Then, x is part of a core if and only if the intersection of the sets N(ct) has size at least i.
We will use this fact to determine which of the fans that we have chosen qualify as part of a community. If the fan qualifies, then we output the community; otherwise we output nothing. In either case, we can prune the fan. It turns out the the condition in Fact 2 can be verified efficiently by batching many fans together. This is exactly what we do.
We maintain a set S(x) corresponding to each fan x. The goal is that at the end of the computation, the set corresponding to the fan x will be the intersection of the sets N(ct) specified in Fact 2, above. Stream through the edges sorted by destination. For each destination y check if it is in the small index. If so, then there is at least one fan of outdegree exactly j adjacent to it. If not, edges adjacent to y are meaningless in the current pass. Assume, therefore that y is in the index. For each degree j fan x adjacent to y, intersect the set of fans adjacent to y with the set corresponding to x. That is, S(x) is intersected with N(y). Recall that since the edges are sorted by destination, N(y) is available as a contiguous sequence in the scan.
At the end of this batched run, S(x) is the set required to verify Fact 2 for every x. For vertices x whose sets, S(x), have size at least i, the S(x) corresponds to the fans in the cores they belong in. In this case, we can output the community immediately. In either case, we can prune x. We can also (optionally) prune all the fans that belong in some community that we output. Thus, we get the following interesting fact. Inclusion-exclusion pruning can be reduced to two passes over the dataset separated by a sort operation.
The following statements apply to all the pruning steps up until this point:
Theorem 3: Given
any graph, no yet-unidentified cores are eliminated by the above pruning
steps.
Theorem 4: The running time of the above pruning steps is linear in the size of the input plus the number of communities produced in these steps.
Theorem 3 states that the set of cores generated so far is complete in that no cores are missed. This is not always a desirable property, especially if many "false positives" are produced. However, our results in Section 4 show that we do not suffer from this problem. Theorem 4 shows that our algorithms up until this point are output-sensitive: the running time (besides being linear in the size of the input) grows linearly in the size of the output. In other words, we spend constant time per input item that we read, and constant time per core we produce (if we view i and j as constants independent of the size of the input).
http://chestnut.brown.edu/Students/Muslim_Students/Org.html
http://wings.buffalo.edu/sa/muslim/resources/msa.html
http://gopherhost.cc.utexas.edu/students/msa/links/links.html
Table 1 shows the number
of cores that were output during inclusion-exclusion pruning, for various
values of i
and
j
. Communities with any fixed value
of
j are largely disjoint due to the way the inclusion-exclusion
pruning is done. Thus, our trawling has extracted about 135K communities
(summing up communities with j = 3).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Next we filtered away nepotistic cores. A nepotistic core is one where some of the fans in the core come from the same web-site. The underlying principle is that if many of the fans in a core come from the same web-site, this may be an artificially established community serving the ends (very likely commercial) of a single entity, rather than a spontaneously-emerging web community. For this purpose, the following definition of "same web-site" is used. If the site contains at most three fields, for instance, yahoo.com, or www.ibm.com then the site is left as is. If the site has more than three fields, as in www3.yahoo.co.uk, then the first field is dropped. The last column in the table above represents the number of non-nepotistic cores. As can be seen the number of nepotistic cores is significant, but not overwhelming - on our 18-month old crawl. About half the cores pass the nepotism test.
We would expect the number
of cores in the current web to be significantly higher.
Fix j. Start with
all (1, j) cores. This is simply the set of all vertices with outdegree
at least j. Now, construct all (2, j) cores by checking every
fan which also cites any center in a (1, j) core. Compute all (3,
j) cores likewise by checking every fan which cites any center in a
(2, j) core, and so on. Figure 2 plots the number of resulting cores
as a function of i and j, based on the subgraph remaining
after the (3, 3) pruning step. Note that, in contrast to the pruning
algorithm, this algorithm will output cores and all their subcores. We
have normalized so that the count of (i,j) cores includes only non-overlapping
cores, but the (i,j) cores may overlap with the (i',j') cores.
The number of (3, 3) cores is about 75K, and is an upper bound on
the total number of disjoint cores of size (3,3) or greater remaining
after inclusion-exclusion pruning.
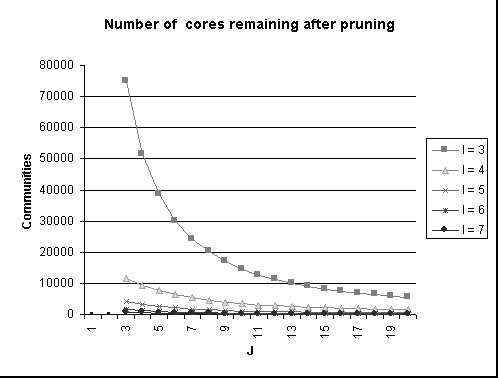
Figure 2: Number of cores
remaining after pruning.
Curiously, the number (75K) is smaller than, though comparable to, the number of cores found by the inclusion-exclusion step (about 135K). Thus, we note that there are approximately 200K potential communities in our dataset; in fact, as our results in the next section show, it appears that virtually all of these cores correspond to real communities (rather than coincidental occurrences of complete bipartite subgraphs). Given that the dataset is about a year and a half old, it seems safe to conjecture that there are at least as many communities in the web today.
In this section we describe our preliminary evaluations of the communities that have been trawled by our system; as a first step, we rely on manual inspection to study the communities that result. (In the longer run we need a mechanized process for dealing with over a hundred thousand communities. This raises significant challenges in information retrieval research.) For this manual inspection, we have picked a random sample of 400 cores (200 (3,3)cores and 200 (3,5) cores) from our list.
Fossilization. Given that we worked with an 18-month old crawl, the first question we studied was how many of the community cores that we had discovered were recoverable in today's web. A fossil is a community core not all of whose fan pages exist on the web today. To our surprise, many of the community cores were recoverable as communities in today's web. Of the 400 communities in the random sample, 122 -- or roughly 30% were fossilized. The rest were still alive. Given prevailing estimates of the half-life of web pages (well under 6 months), we found it surprising that fan pages corresponding to community cores are significantly longer-lived. This seems to be yet another indicator of the value of resource collections in the web and consequently, the robustness of methods such as ours.
Communities. The next
question was in studying the communities themselves. To give a flavor
of communities we identify, we present the following two examples.
The first one deals with Japanese pop singer Hekiru Shiina.
The following are the fans of this community.
http://awa.a-web.co.jp/~buglin/shiina/link.html
http://hawk.ise.chuo-u.ac.jp/student/person/tshiozak/hobby/heki/hekilink.html
http://noah.mtl.t.u-tokyo.ac.jp/~msato/hobby/hekiru.html
The next example deals with
Australian fire brigade services. The following are the fans of this
community.
http://maya.eagles.bbs.net.au/~mp/aussie.html
http://homepage.midusa.net/~timcorny/intrnatl.html
http://fsinfo.cs.uni-sb.de/~pahu/links_australien.html
A more extensive annotated list of some the communities that we find can be viewed here .
Reliability. The next question was what fraction of the live cores were still cogent in that they covered a single characterizable theme. We found the cores to be surprisingly reliable. Of the 400 cores, there were 16 coincidental cores -- a collection of fan pages without any cogent theme unifying them. This amounts to just 4% of our trawled cores. Given the scale of the web and our usage of link information alone, one might expect a far larger fraction of accidental communities. It appears that our many careful pruning steps paid off here. Given these sample results, one can extrapolate that the fraction of fossils and coincidences together account for less than 35% of the cores that were trawled. In other words, we estimate that we have extracted some 130K communities that are alive and cogent in today's web.
Recoverability. The
core is only part of the community. For communities that have not fossilized,
can we recover today's community from the core that we extracted? A method
we use for this purpose is to run the Clever search engine on the community
core, using the fans as exemplary hubs (and no text query). For details
on how this is done, see Chakrabarti et. al. (2) 98,
and Kumar et. al. 98. Table 2 below shows
the output of Clever (top 15 hubs and authorities)
run on one of our cores, which turns out to be for Australian fire brigades.
A more extensive list can be found here.
Table 2: A community of Australian fire brigades.
Quality. How many of our communities are unknown to explicit ontological efforts? We found that of the sampled communities, 56% were not in Yahoo! as reconstructed from our crawl and 29% are not in Yahoo! today in any form whatsoever. (The remaining are present in Yahoo! today, though in many cases Yahoo! has only one or two URL's in its listing whereas our process frequently yields many more. We interpret this finding as a measure of reliability of the trawling process, namely, that many of the communities that we had found emerging 18 months ago have now emerged. Also, none of the trawled communities appears in less than the third level of the Yahoo! hierarchy, with the average level (amongst those present in Yahoo!) being about 4.5 and many communities that were as deep as 6 in the current Yahoo! tree. We believe that trawling a current copy of the web will result in the discovery of many more communities that will become explicit in the future.
Open problems. The dominant open problems are automatically extracting semantic information and organizing the communities we trawl into useful structure. Another interesting problem is to trawl successive copies of the web, tracking the sociology of emerging communities.
 Prabhakar
Raghavan received his Ph.D. in Computer Science from the University
of California, Berkeley in 1986. Since then he has been a Research Staff
Member at IBM Research, first at the Thomas J. Watson Research Center in
Yorktown Heights, NY, and since 1995 at the Almaden Research Center in
San Jose, California. He is also a Consulting Professor at the Computer
Science Department, Stanford University. His research interests include
algorithms, randomization, information retrieval and optimization. He is
the co-author of a book Randomized
Algorithms and numerous technical papers. He has served on the editorial
boards and program committees of a number of journals and conferences.
Prabhakar
Raghavan received his Ph.D. in Computer Science from the University
of California, Berkeley in 1986. Since then he has been a Research Staff
Member at IBM Research, first at the Thomas J. Watson Research Center in
Yorktown Heights, NY, and since 1995 at the Almaden Research Center in
San Jose, California. He is also a Consulting Professor at the Computer
Science Department, Stanford University. His research interests include
algorithms, randomization, information retrieval and optimization. He is
the co-author of a book Randomized
Algorithms and numerous technical papers. He has served on the editorial
boards and program committees of a number of journals and conferences.
 Sridhar
Rajagopalan has received a B.Tech. from the Indian Institute of Technology,
Delhi, in 1989 and a Ph.D. from the University of California, Berkeley
in 1994. He spent two years as a DIMACS postdoctoral fellow at Princeton
University. He is now a Research Staff Member at the IBM Almaden Research
Center. His research interests include algorithms and optimization, randomization,
information and coding theory and information retrieval.
Sridhar
Rajagopalan has received a B.Tech. from the Indian Institute of Technology,
Delhi, in 1989 and a Ph.D. from the University of California, Berkeley
in 1994. He spent two years as a DIMACS postdoctoral fellow at Princeton
University. He is now a Research Staff Member at the IBM Almaden Research
Center. His research interests include algorithms and optimization, randomization,
information and coding theory and information retrieval.
 Andrew
Tomkins received his BSc in mathematics and computer science from MIT
in 1989, and his PhD from CMU in 1997. He now works at the IBM Almaden
Research Center in the Principles and Methodologies group. His research
interests include algorithms, particularly online algorithms; disk scheduling
and prefetching; pen computing and OCR; and the world wide web.
Andrew
Tomkins received his BSc in mathematics and computer science from MIT
in 1989, and his PhD from CMU in 1997. He now works at the IBM Almaden
Research Center in the Principles and Methodologies group. His research
interests include algorithms, particularly online algorithms; disk scheduling
and prefetching; pen computing and OCR; and the world wide web.